“Une plus grande connaissance du danger permet une plus grande sécurité.” – Benoît Mandelbrot.
Plusieurs causes sont à l’origine de la crise financière des années 2007-2008. Certains évoquent l’excès d’optimisme des banques et des emprunteurs (à risque) dans un marché immobilier haussier. D’autres accusent l’ingénierie financière des banques et le mécanisme de rémunération des commerciaux qui incitaient à une prise de risque toujours plus élevée. Enfin, d’autres encore évoquent la politique monétaire trop accommodante de la Réserve fédérale américaine.
Au fond, l’origine est toujours la même : l’incompréhension du fonctionnement des marchés financiers. Et plus précisément, l’incapacité à évaluer et à gérer correctement le risque. En bref, cela signifie que le modèle mental utilisé pour représenter la volatilité n’est pas opérationnel.
Dans le livre Une approche fractale des marchés, le mathématicien Benoît Mandelbrot met en évidence les faiblesses des modèles actuels. Mais surtout, il propose un nouvel outil pour mieux analyser et gérer l’incertitude sur les marchés : les fractales.
Dans cet article, je vais vous présenter les idées principales concernant la gestion des risques.
Et puisque nous parlons du risque, rappelons d’abord rapidement les différentes approches du risque sur les marchés financiers :
Le modèle de l’analyse fondamentale : les raisons du mouvement d’une action sont à rechercher dans l’étude de la société, de son marché général et de l’environnement économique global.
Le modèle de l’analyse technique : l’étude des graphiques des cours et de différents indicateurs permet de prévoir (ou du moins de réagir rapidement à) l’évolution des marchés.
La modélisation financière (la finance moderne) : Les prix ne sont pas prévisibles mais leurs fluctuations peuvent être décrites par des lois mathématiques. Cette approche utilisée par les banques capitalise sur la puissance de calcul des ordinateurs et les techniques statistiques (algorithmes).
Deux principaux types de hasard
Il y a deux types de hasard : le hasard modéré et le hasard sauvage.
L’univers du hasard modéré (que Nassim Taleb appelle le “Médiocristan”) est un lieu plutôt prévisible qui est soumis à la loi du collectif. Par exemple, les historiens modernistes expliquent l’histoire en disant que le cours des événements est le résultat des nombreuses actions réalisées par des individus oubliés. Dans cette vision, les changements importants sont le résultat d’un grand nombre de petites actions.
L’univers du hasard sauvage (l’“Extrêmistan”, pour Taleb) est soumis à la loi du singulier. Et donc de l’accidentel et de l’imprévu. Pour les historiens traditionalistes, l’histoire est forgée par quelques grands hommes (César, Napoléon, Einstein, etc.). Ici, les changements importants sont le résultat d’un seul événement extrême. Vous pouvez penser aux lois de puissance comme le 80/20.

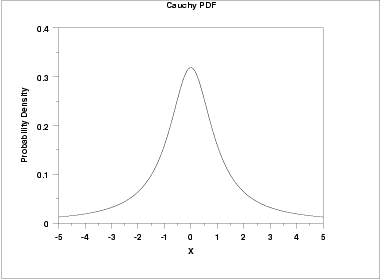
Ces deux types de hasard correspondent à deux visions du monde complètement différentes :
Dans le hasard modéré, la puissance est collective. La petite queue de distribution fait que les actions éloignées de la moyenne sont limitées et pèsent peu sur l’ensemble.
Dans le hasard sauvage, les queues de distribution sont extrêmement longues. Cela signifie que de nombreuses valeurs peuvent être très éloignées de la moyenne et avoir énormément d’impact. Dans ce cas, la puissance est individuelle.
Je vous invite à prendre deux minutes afin de voir quel type de hasard a eu le plus d’effet sur votre vie. Cela vous permettra de sentir intuitivement quelle est la forme de hasard qui a le plus d’impact dans les marchés financiers.
#1 : Les erreurs de la finance moderne
Mandelbrot est particulièrement sceptique concernant les hypothèses de la théorie financière qui est utilisée par les banques. Ces hypothèses supposent que les évolutions des cours financiers obéissent au hasard modéré. Pourtant, dans les faits, on observe qu’ils sont soumis aux lois du hasard sauvage. Voici les principales hypothèses qu’il critique :
Hypothèse 1 : les investisseurs sont des supercalculateurs rationnels
Dans la réalité, les investisseurs ne sont pas des supercalculateurs qui cherchent à maximiser leur utilité. Par exemple, les investisseurs ont généralement une aversion au risque : ils préfèrent un gain sûr à un gain éventuel plus important. Et ils ont également une aversion à la perte : la crainte de perdre est plus forte que l’envie de gagner (même dans le cas où la probabilité de gain est plus forte). Cette forte asymétrie au risque handicape notre raisonnement.
Hypothèse 2 : tous les investisseurs se ressemblent
Dans la pratique, tous les investisseurs ne se ressemblent pas. Ils n’ont pas le même horizon de temps, ni le même capital de départ, ni les mêmes stratégies, etc.. Il y a notamment des investisseurs de valeur (ceux qui recherchent les titres sous-cotés) et il y a des traders (ceux qui exploitent les configurations techniques). La théorie classique ne tient pas compte des différents profils d’investissement que l’on rencontre dans la réalité.
Hypothèse 3 : les variations de cours sont pratiquement continues
La théorie suppose que les cours varient doucement d’une valeur à l’autre. Ils fonctionneraient de façon continue comme une température. Pourtant, tout investisseur sait que les cours fonctionnent par saut. La discontinuité des variations de prix est une propriété essentielle de la finance.
Hypothèse 4 : les variations de cours suivent un mouvement brownien
Le mouvement brownien est un terme issu de la physique qui désigne le mouvement d’une molécule dans un milieu uniformément chaud. Les financiers utilisent ce modèle pour décrire les variations de prix. Le souci c’est que ce modèle présuppose des critères qui ne sont pas valables pour les cours financiers :
L’indépendance des variations de prix. Dans les faits, les variations de prix ne sont pas indépendantes. Les prix ont une “mémoire”.
La stationnarité statistique des variations de cours. Dans les faits, les variations de cours sont changeantes (il existe plusieurs tendances différentes).
Distribution normale des variations de cours. Dans la réalité, les variations de cours ne suivent pas une loi de Gauss (qui représente le hasard modéré). Sinon, cela voudrait dire que la plupart des variations sont faibles. Et que les variations extrêmes de prix sont non seulement rares mais également prévisibles.
Pourquoi le secteur financier persiste dans ses erreurs ?
Le pragmatisme est la philosophie du secteur financier. Les économistes et les financiers sont pour la plupart conscients des limites de leurs modèles. Mais comme les modèles fonctionnent 95% du temps, c’est-à-dire hors cas extrême, les banques continuent de les utiliser.
Bien sûr, ils prennent conscience que les gains réalisés sur la période stable (95% du temps) peuvent s’effacer lors des crashs. Mais, étant donné que ces modèles sont très pratiques à utiliser (peu de paramètres + leur côté intuitif), ils les conservent en les ajustant à la marge après coup.
Les lecteurs de cet article ont également apprécié l’article suivant : Antifragile : Comment prospérer dans un monde d’incertitude
Cependant, il faut noter que, suite aux différentes crises financières, l’attention du secteur commence de plus en plus à se tourner vers l’étude des extrêmes. Ils prennent conscience de l’importance du hasard sauvage sur les cours. Autant pour des questions de régulation (protection du capital) que pour des questions d’opportunisme financier (réalisation de profits).
Pour conclure sur les erreurs de la finance moderne, gardons en mémoire le rappel de Mandelbrot : quand les architectes navals concevaient leurs bateaux, “ils ne concevaient pas leurs bateaux uniquement pour les 95% de jours où la mer est clémente mais aussi pour les 5% restants, lorsque la tempête souffle et que leur talent est mis à rude épreuve“.
#2 : Les solutions du modèle fractal
Qu’est-ce qu’une fractale ?
Avant Mandelbrot, la géométrie, vue comme l’étude des formes de la nature, étudiait le lisse. L’aspect rugueux – ou plus précisément l’irrégularité – de la nature était considéré comme une imperfection. Et il n’était donc pas pris en considération.
D’où les représentations géométriques avec des triangles parfaits, des lignes, des carrés, etc. alors que nulle part dans la nature, nous ne trouvons ce type de formes parfaites. Les montagnes ne sont pas exactement triangulaires; vous ne rencontrerez quasiment jamais de lignes parfaitement droites.
L’ancienne géométrie euclidienne, spécialisée dans l’étude du lisse (une forme idéalisée de la nature) apparaît donc comme une invention des mathématiciens complètement déconnectée de la nature.
Pour étudier la nature réelle – et non pas fantasmée – Mandelbrot a renversé cette perspective. Sa théorie fractale considère le rugueux comme l’essence même de beaucoup d’objets de la nature. Pour décrire cette propriété fondamentale, il a inventé un nouveau concept : la géométrie fractale.

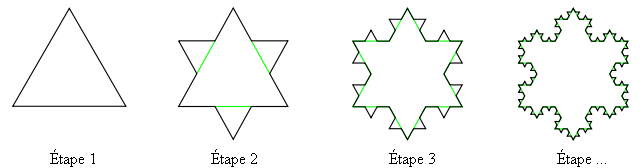
“Une fractale possède une forme spéciale d’invariance ou de symétrie qui relie le tout à ses parties : le tout peut être divisé en parties plus petites, chacune répétant le tout comme en écho.” – Mandelbrot.
Quittons la nature pour constater que nous retrouvons également les propriétés fractales dans la vie sociale. Prenons la loi de puissance de Pareto, le 80/20. Par exemple, cette loi nous dit que 80% des richesses sont détenues par 20% des personnes. Cette loi est elle-même fractale. C’est-à-dire qu’on peut l’appliquer à elle-même. Ainsi, 64% des richesses sont détenues par 4% des personnes. 50% des richesses sont détenues par 1% des personnes, etc.
De nouveaux principes pour rectifier les erreurs de la finance moderne
1/ Les marchés sont turbulents. Les prix fonctionnent comme un processus turbulent “dont les parties obéissent de manière fractale à une loi d’échelle”.
2/ Les marchés sont bien plus risqués que les théories standards ne l’imaginent. Dans un environnement aussi extrême, la notion de performance moyenne n’a pas de sens. Ce qui compte ce sont les valeurs extrêmes des bénéfices et des pertes. Plus particulièrement, le risque de ruine est ce qui doit être évité à tout prix.
3/ Tout est une question de timing. Les gains et les pertes se concentrent dans de petits intervalles de temps car la volatilité est très concentrée. Le conseil (prudent) que l’on entend en général est de ne pas essayer de “timer” le marché. Mais, en fait, il est essentiel d’essayer d’estimer le bon moment pour acheter ou vendre. Le moment précis d’achat compte plus que la moyenne. Ici, nous voyons que l’auteur critique la méthode DCA (Dollar cost averaging ou investissement programmé) qui consiste à fractionner son achat sur la durée pour diminuer la volatilité (qui est considérée non concentrée ici).
4/ Les prix sautent régulièrement. Les marchés financiers ne sont pas lisses. Ils “cassent” par moment. Ils sont sauvages, ils sont fractals. Il s’agit d’une différence fondamentale entre l’économie et la physique classique (“la nature ne fait pas de sauts”).
5/ Sur les marchés, le temps est flexible. Chaque investisseur possède son propre horizon d’investissement. Les fractales règlent cela car les variations de prix suivent une loi d’échelle avec le temps : en termes statistiques, les risques sur une journée sont identiques à ceux sur une semaine.
6/ Les marchés, partout et à toutes les époques, fonctionnent de manière identique.
7/ Les marchés sont incertains et les bulles inévitables. C’est la conséquence du fait que la distribution des variations de prix suit une loi d’échelle.
8/ Les marchés sont trompeurs. Les investisseurs tentent de distinguer des configurations là où il n’en existe pas. Cependant, parfois, la dépendance à long terme des prix (la mémoire) peut créer des variations persistantes (qui se renforcent) ou anti-persistantes (qui se contredisent).
9/ Prévoir le cours peut être dangereux mais on peut estimer les probabilités de volatilité future.
Le mot de la fin
Pour finir, je n’ai qu’une seule chose à vous dire : si vous vous intéressez à la gestion du risque et/ou aux investissements, je vous recommande fortement la lecture du livre Une approche fractale des marchés. L’approche fractale des marchés de Mandelbrot ouvre la voie à une toute nouvelle conception du risque financier qui, à n’en pas douter, fera date.
A retenir : La géométrie fractale est un modèle mental qui permet de mieux analyser la nature sauvage en générale et les risques des marchés financiers en particulier.
Vous avez apprécié cet article ? Vous êtes libre de vous abonner à ma newsletter hebdomadaire pour ne manquer aucun article similaire.
Pour copier et partager : https://mikaelecanvil.com/approche-fractale-marches/
NB. 1 : Un exemple pour illustrer la notion de loi d’échelle. Cette loi signifie que le comportement à un certain niveau est le même comportement qu’à un autre niveau. Dit autrement, chaque univers du système obéit aux mêmes lois. Exemple : “la probabilité d’avoir un revenu supérieur à dix milliards, quand vous gagnez plus d’un milliard, est la même que celle d’avoir un revenu supérieur à dix millions quand vous gagnez plus d’un million”.
NB. 2 : Il me semble que nous pouvons aussi concevoir la poursuite des objectifs comme un processus fractal : à chaque nouvel objectif atteint, la joie est courte puis le jeu recommence à une nouvelle échelle. Les innovations technologiques fonctionnent également de façon fractale : les disruptions sont les “cassures”. D’ailleurs, si l’on pousse encore plus loin, la vie elle-même peut sembler fractale… “Tout est dans tout“.




1 comment